birthdayboy224Lvl 2- Windows
Captain_Jack_Sparrow the answer is clearly 0
0 divided by 0 is?
DragonFireGamesLvl 11- Edited
It can be a lot of things depending on the context:
For example:
In the function f(x) = x/x, the limit as x approaches 0 from both sides of the graph of f(x) is 1.
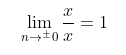In the function f(x) = 0/x, the limit as x approaches 0 from both sides of the graph of f(x) is 0.
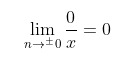Since 0/0 cannot be both 1 and 0, it is an indeterminate form.
In fact, for any number n, this can be generalized to: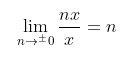
This means 0/0 would have to be all numbers at the same time, which makes no sense.
PS: This is also the logic behind 1/0 being undefined. In the function f(x) = 1/x, the limit as x approaches 0 from the right is infinity whilst the limit as x approaches 0 from the left is -infinity. This is about as dumb as IEEE floating point: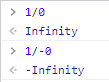 
You can, however, define an unsigned infinity: 
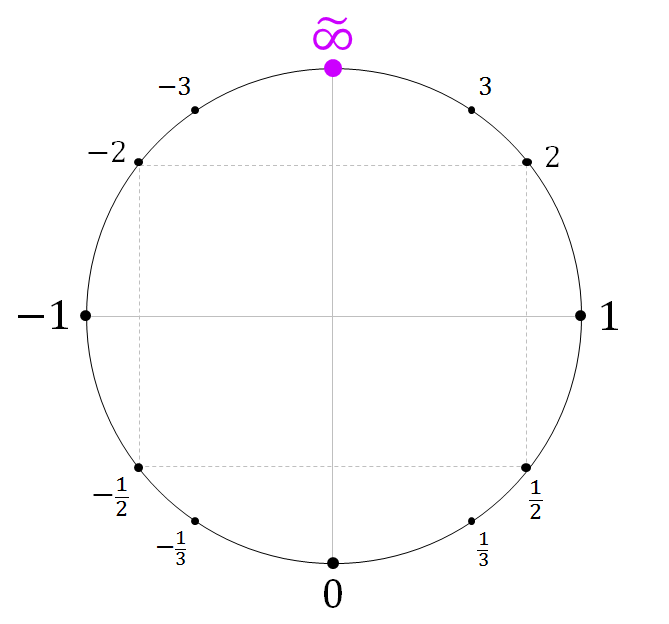which allows 1/0 and -1/0 to be an unsigned infinity.
PSS: The graphs for context:
altZanyLvl 1- Windows
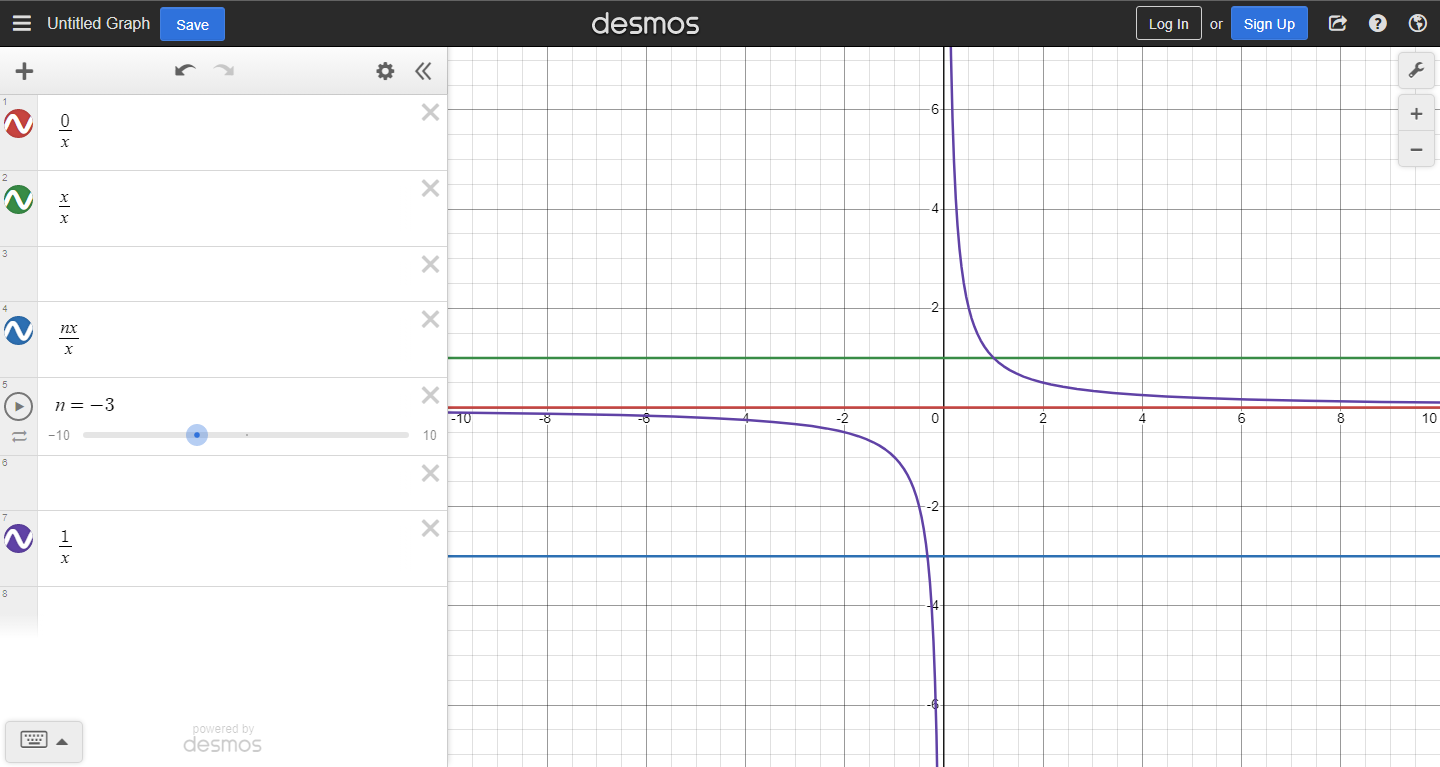
I used Desmos in 7th grade for math.
MonsterYT_DaGamerLvl 8- Edited
- Android
If 2/2 = 1, and 1/1 = 1, then 0/0 = 1.
(very real)
- altZanyLvl 1
- Windows
MonsterYT_DaGamer I don't think that's how it works...
INTERNECIONLvl 62- Edited
- Android
Ah yes when I have literally no slices of pizza to share with literally nobody in the room, there's one slice for each person
- DragonFireGamesLvl 11
MonsterYT_DaGamer
if 0/2 = 0, and 0/1 = 0, then 0/0 = 0
(very real)
ackvonhuelioLvl 41
DragonFireGames
just because lim x -> 0 of 0/x is 0 doesnt mean f(0) is 0
VarrienceLvl 25
[x]
Player version
Player FPS
Video type
Video url
Video resolution
Video duration
Video load failed
i got my evaluation from here.... since i think you probably can't solve it without imaginary numbers i thought the answer would be infinite.... but I've never been good at math theroy so....
- DragonFireGamesLvl 11
ackvonhuelio True, but it is the only way to make f continuous, and continuity is a very useful property for a function to have. If someone wants to arbitrarily define a value for f(0) that makes f continuous, using a limit is the best way to do so. 0/0 is undefined. But if someone wants to draw useful conclusions about it, using the limit is a good way to do that.
In the function f(x)=(x+5)(x-3)/(x+5), f cannot be simplified to just x-3 because there is a hole at f(-5). However, if we define f(-5) to be -8 using the left and right side limit, that allows us to simplify f and get rid of the hole. This uses limits to draw useful conclusions about f.
