It can be a lot of things depending on the context:
For example:
In the function f(x) = x/x, the limit as x approaches 0 from both sides of the graph of f(x) is 1.
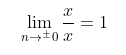 In the function
In the function f(x) = 0/x, the limit as x approaches 0 from both sides of the graph of f(x) is 0.
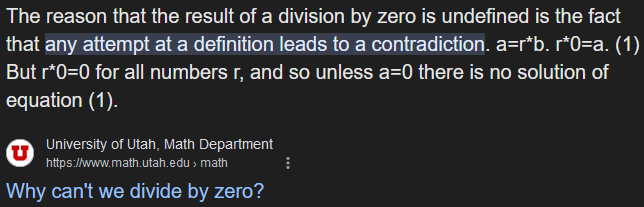
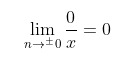 Since 0/0 cannot be both 1 and 0, it is an indeterminate form.
Since 0/0 cannot be both 1 and 0, it is an indeterminate form.
In fact, for any number n, this can be generalized to: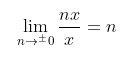 This means 0/0 would have to be all numbers at the same time, which makes no sense.
This means 0/0 would have to be all numbers at the same time, which makes no sense.
PS: This is also the logic behind 1/0 being undefined. In the function f(x) = 1/x, the limit as x approaches 0 from the right is infinity whilst the limit as x approaches 0 from the left is -infinity. This is about as dumb as IEEE floating point: 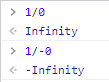 You can, however, define an unsigned infinity:
You can, however, define an unsigned infinity: 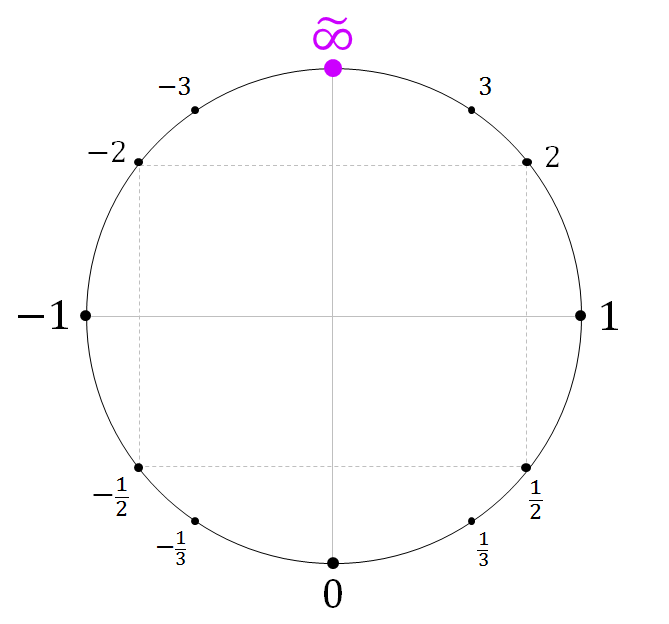 which allows 1/0 and -1/0 to be an unsigned infinity.
which allows 1/0 and -1/0 to be an unsigned infinity.
PSS: The graphs for context:
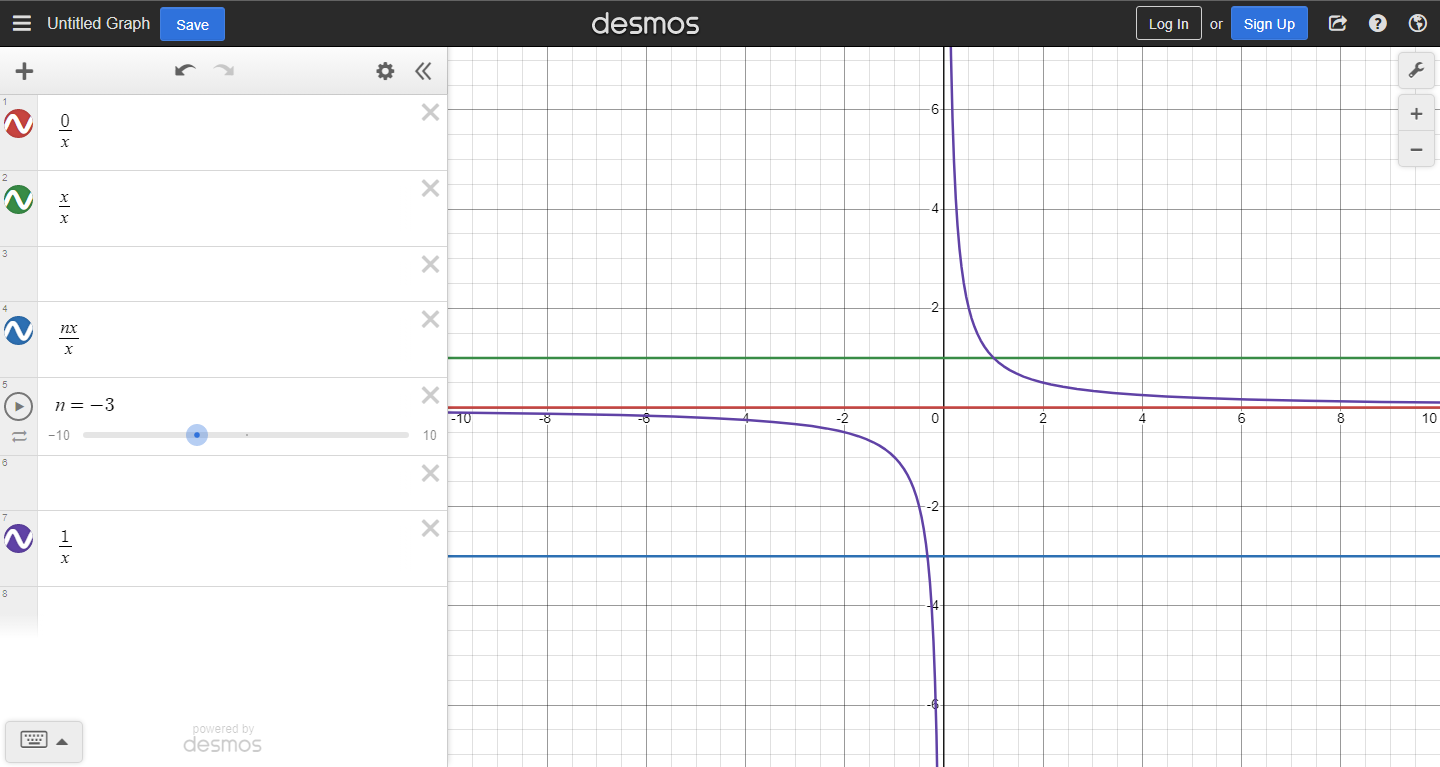

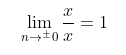 In the function
In the function 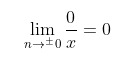 Since 0/0 cannot be both 1 and 0, it is an indeterminate form.
Since 0/0 cannot be both 1 and 0, it is an indeterminate form.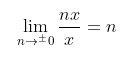 This means 0/0 would have to be all numbers at the same time, which makes no sense.
This means 0/0 would have to be all numbers at the same time, which makes no sense. You can, however, define an unsigned infinity:
You can, however, define an unsigned infinity:  which allows 1/0 and -1/0 to be an unsigned infinity.
which allows 1/0 and -1/0 to be an unsigned infinity.